Satz des Pythagoras durch analytische Geometrie beweisen YouTube

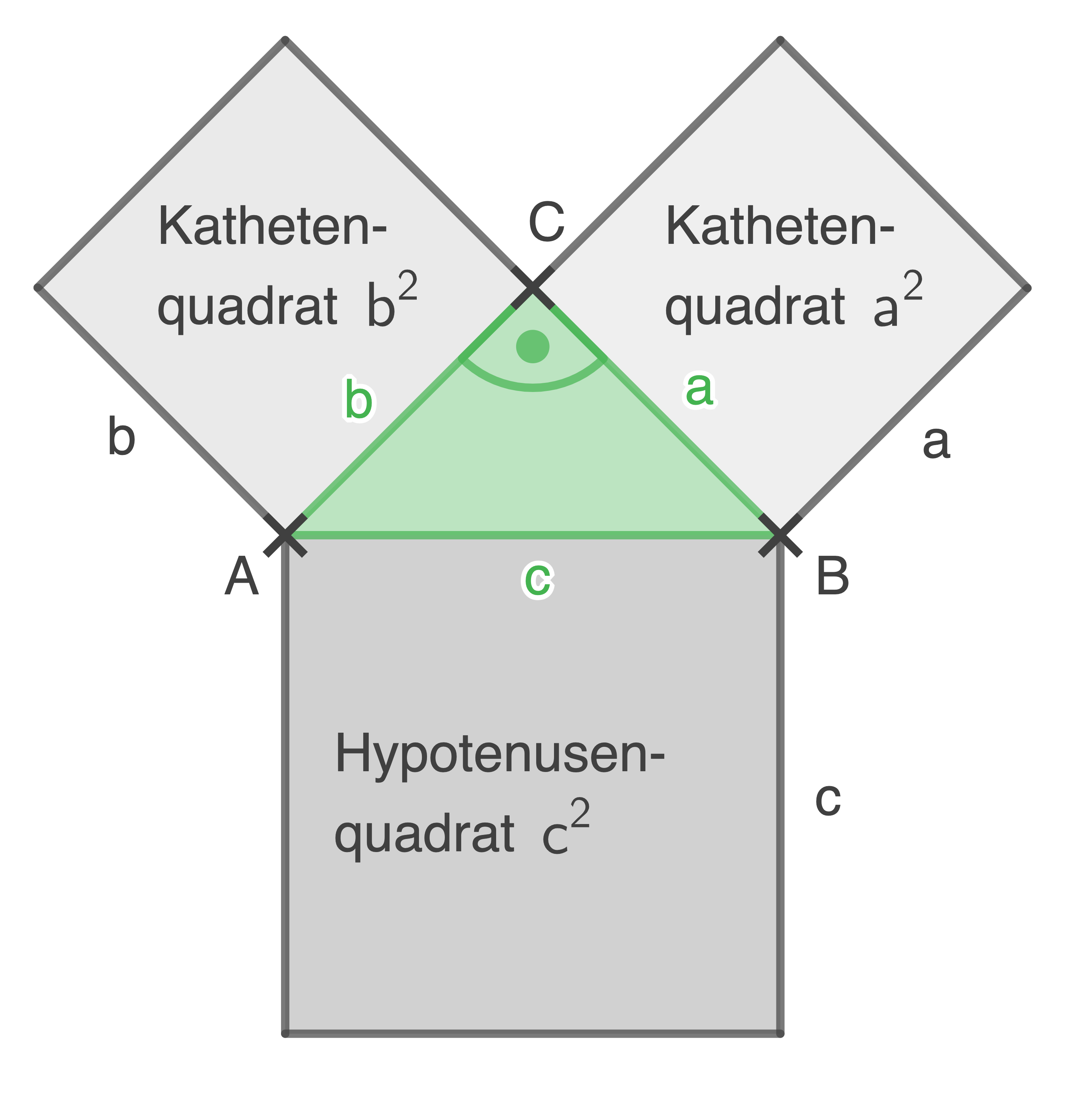
Satz des Pythagoras. Der Satz des Pythagoras (auch Hypotenusensatz) ist einer der fundamentalen Sätze der euklidischen Geometrie. Er besagt, dass in allen ebenen rechtwinkligen Dreiecken die Summe der Flächeninhalte der Kathetenquadrate gleich dem Flächeninhalt des Hypotenusenquadrates ist.
Satz des Pythagoras Erklärung

Und was sagt er genau aus? In diesem Artikel erklären wir dir, was es mit dem Satz des Pythagoras auf sich hat und zeigen dir anhand von einigen Beispielen, für welche Art von Aufgaben der Satz sehr hilfreich ist. Satz des Pythagoras Grundlagenwissen.
www.mathefragen.de Satz des pythagoras

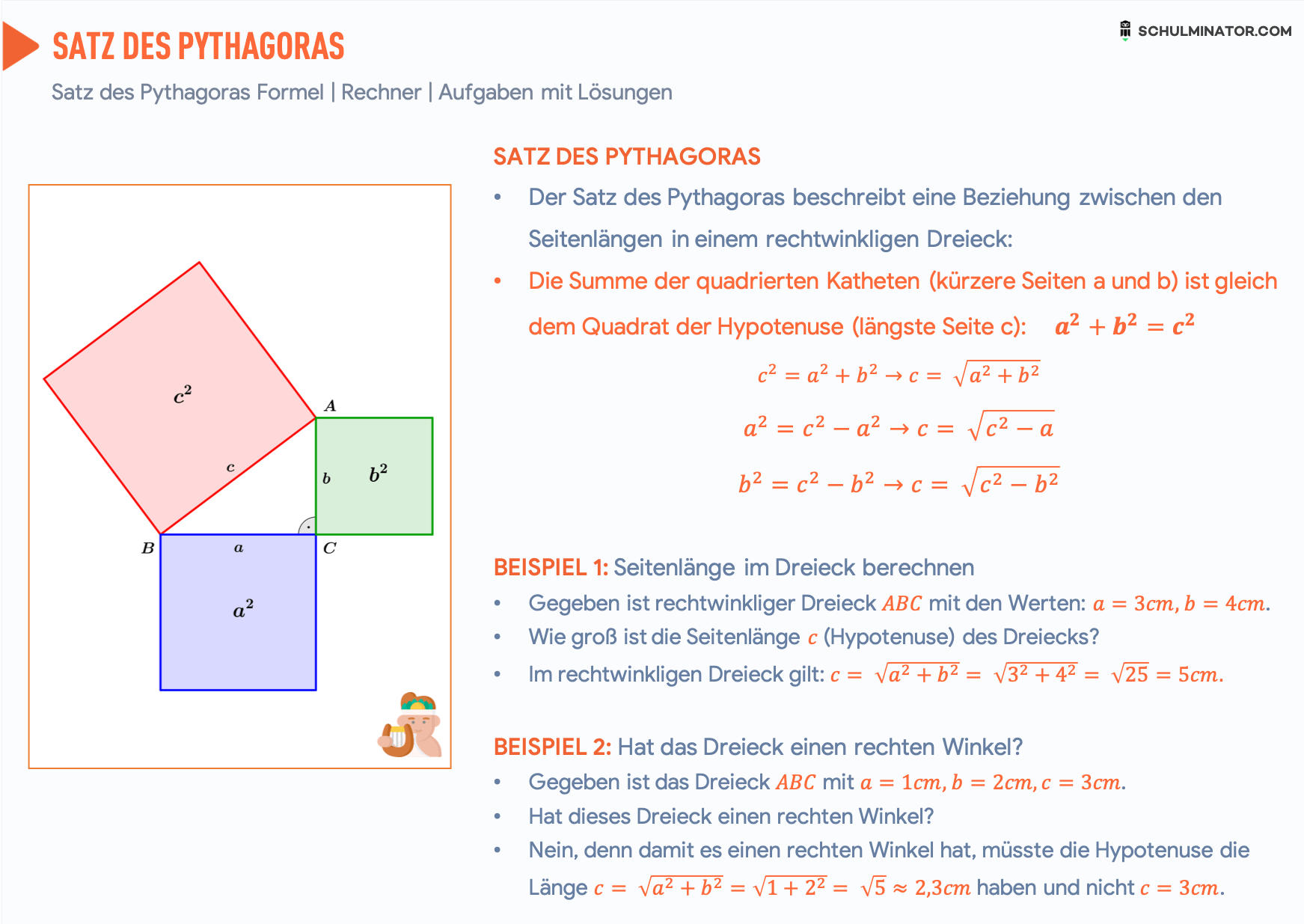
Der Satz des Pythagoras ist eine Formel, mit der du die Seitenlängen eines rechtwinkligen Dreiecks berechnen kannst. Die Formel lautet: a² + b² = c². Dabei sind a und b die kurzen Seiten im Dreieck. Sie liegen am 90°-Winkel und heißen Katheten . c ist die längste Seite im Dreieck. Sie liegt gegenüber vom rechten Winkel und heißt Hypotenuse.
Satz Des Pythagoras Winkel Berechnen
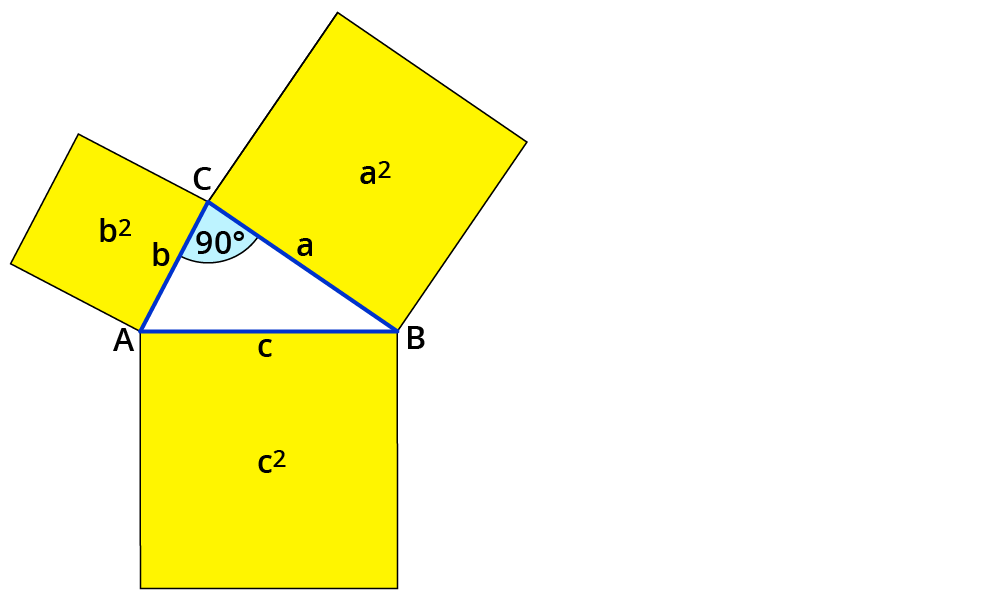
Englisch. Anwendungsaufgaben mit dem Pythagoras. Einleitung. Viele Anwendungen kannst du mithilfe des Satzes von Pythagoras berechnen. Zeichne zuerst immer eine Skizze. Markiere den rechten Winkel und alle gegebenen Längen. So siehst du auf den ersten Blick, welche Länge gesucht ist: eine Kathete oder die Hypotenuse. Zur Erinnerung:
Bhaskaras Beweis für den Satz des Pythagoras YouTube
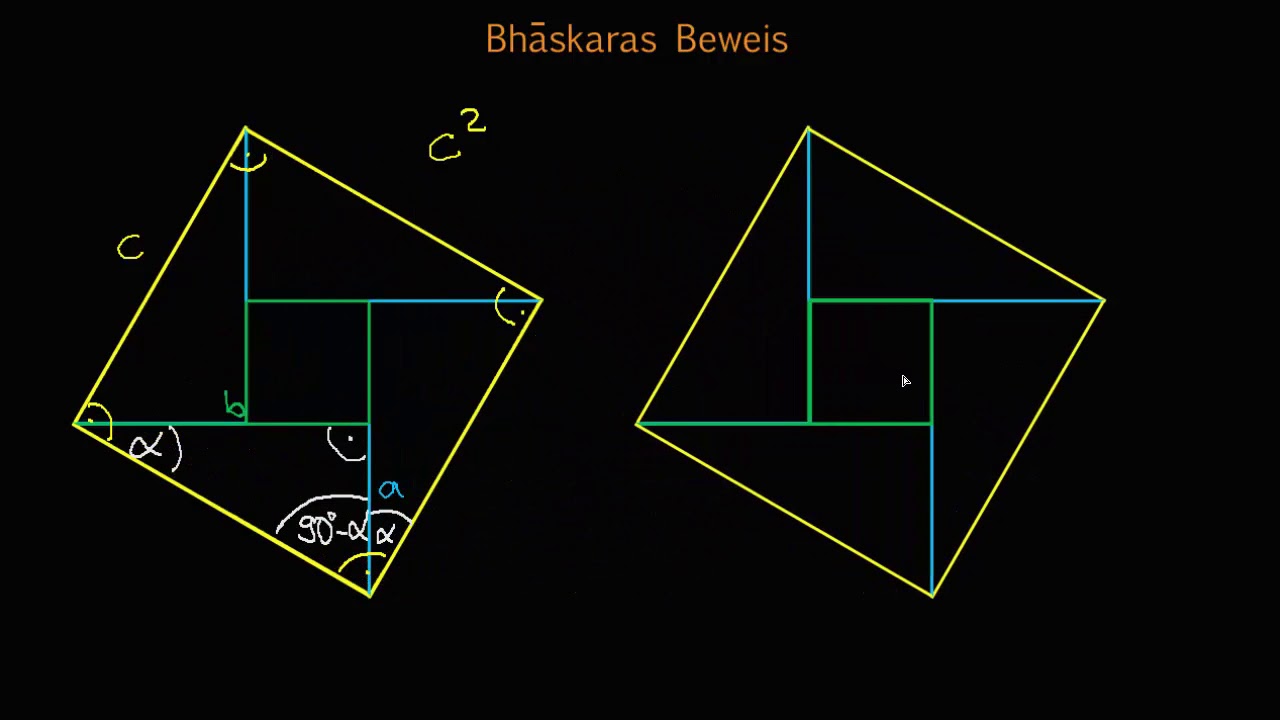
In diesem Video lernst du den Satz des Pythagoras kennen. Wir zeigen dir, wie du die Seitenlängen in einem rechtwinkligen Dreieck einfach berechnen kannst.
Der Satz des Pythagoras für 19.8 EUR sichern

Google Classroom. Über uns. Transkript. Sal verwendet dem Satz des Pythagoras, um die Höhe eines rechtwinkligen Dreiecks mit einer Grundfläche von 9 und einer Hypotenuse von 14 zu finden. Erstellt von Sal Khan und Monterey Institut für Technologie und Bildung. Fragen. Spenden & Danksagungen. Willst du an der Diskussion teilnehmen? Anmelden.
Satzgruppe des Pythagoras Satz des Pythagoras & Höhensatz & Kathetensatz Mathe unterrichten

Aufbau der Zelle. Pflanzliche Organe. Fische, Lurche, Kriechtiere. Klasse 6. Säugetiere. Insekten. Fortpflanzung und Entwicklung bei Pflanzen. Klasse 7. Aufbau des Verdauungssystems. Blut und Blutkreislauf. Zellteilung.
Pythagoras im Alltag
Sie liegt gegenüber dem 90° Winkel. Aufgabe 1: Klick einen unteren Buttons an und beobachte, was passiert. Klick den nächsten Button, nachdem die grüne Umrandung des vorherigen aufgehoben wurde. Vervollständige danach unten den Satz des Pythagoras. a² + b² = c².
Einfach erklärt Satz des Pythagoras YouTube

Der Satz des Pythagoras wird hauptsächlich in folgenden Fällen angewendet: Berechnung fehlender Seitenlängen in rechtwinkligen Dreiecken (durch Auflösen der Formel nach. \col [1]a a, \col [2]b b oder. \col [3]c c)
Satz Des Pythagoras Beispiel
Test 1. Satz des Pythagoras - Anwendungen. Der Satz des Pythagoras und der Abstand zwischen Punkten. Test 2. Beweise des Satzes des Pythagoras. Abschlusstest. Der Satz des Pythagoras beschreibt ein spezielles Verhältnis zwischen den Seiten eines rechtwinkligen Dreiecks. Sogar in der Antike war dieses Verhältnis bekannt.
PPT Der Satz des pythagoras PowerPoint Presentation, free download ID2072852

Mit dem Satz des Pythagoras kannst du Aussagen bezüglich der Seitenlängen und der Quadrate über den Seiten rechtwinkliger Dreiecke treffen. Begriffe in rechtwinkligen Dreiecken: Die Hypotenuse ist die längste Seite des Dreiecks, sie liegt dem 90°-Winkel gegenüber. Die Katheten sind die kürzeren Seiten, die nicht dem 90°-Winkel gegenüber liegen.
Satz des Pythagoras a² + b² = c² Übungen mit Lösungen ObachtMathe YouTube

Sonntag, 02. Dezember 2018 um 15:22 Uhr. Die Herleitung bzw. den Beweis für den Satz des Pythagoras findet ihr hier. Folgende Inhalte werden angeboten: Eine Erklärung, wie man den Satz des Pythagoras herleitet. Beispiele wie man den Satz des Pythagoras beweist. Übungen damit ihr die Gleichung praktisch üben könnt.
Pythagoras fortgeschrittene Aufgaben YouTube

Laut Pythagoras gilt: a 2 + b 2 = c 2. Der Satz des Pythagoras besagt, dass in einem rechtwinkligen Dreieck die Kathetenquadrate (d. h. die Summe der grünen und blauen Fläche) genauso groß sind wie das Hypotenusenquadrat (rote Fläche).
Satz Des Pythagoras Beispiel My XXX Hot Girl
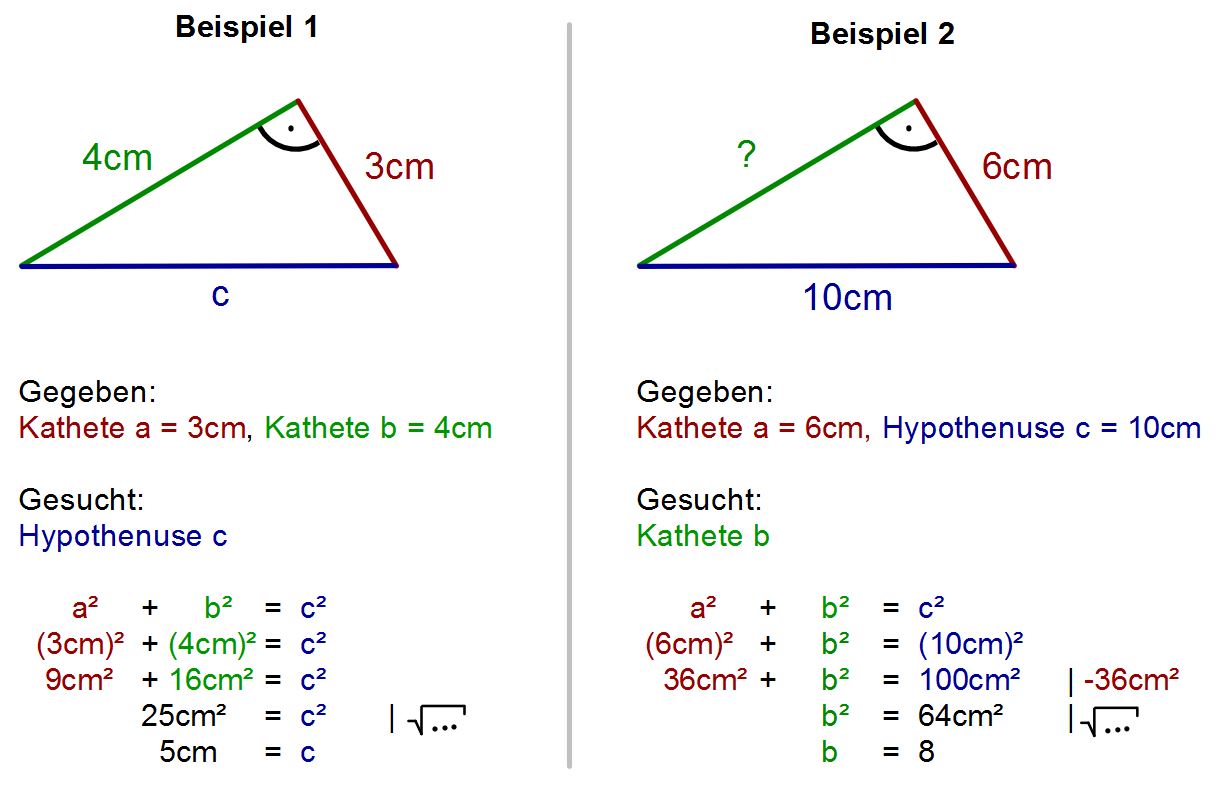
Beispiele für den Satz des Pythagoras: Hypotenuse c berechnen. In diesem Beispiel sind die beiden Katheten a = 6 cm und b = 4 cm gegeben. Mithilfe vom Satz des Pythagoras kann nun die fehlende Hypotenuse berechnet werden. Der Satz des Pythagoras lautet aufgrund der Hypotenuse bei c so: a² + b² = c².
Satz des Pythagoras Beispielaufgabe 2 YouTube

Mit den folgenden Beispielen möchten wir dir dabei helfen, den Satz des Pythagoras noch besser zu verstehen. Durch die Beispiele kannst du sehen, welche Möglichkeiten dir die Formel gibt. Beispiel 1: Aufgabe: In einem rechtwinkligen Dreieck kennst du die Längen der beiden Katheten a und b.
Satz des Pythagoras InstantMathe

Die Kathete a lässt sich zum Beispiel berechnen mit a=\sqrt {c^2-b^2} a = c2 − b2. Weitere Beispielaufgaben. Video mit Beispielrechnungen. Beweis vom Satz des Pythagoras. Pythagoras beschreibt auch Flächengleichheit. Für jede positive Zahl a a beschreibt a^2 a2 die Fläche eines Quadrates mit der Seitenlänge a a.